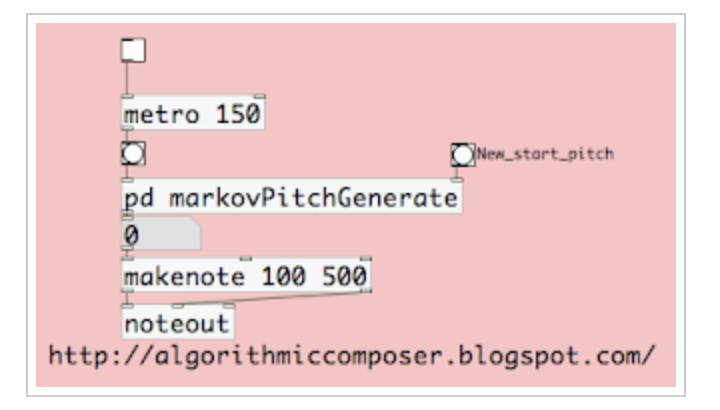
Markov Chain Core in PD
Markov chain
AA stochastic model called a Markov chain or Markov process describes a series of potential occurrences in which each event’s probability solely depends on the state obtained in the preceding event. A discrete-time Markov chain is created from a countably infinite sequence where the chain changes state at discrete time steps (DTMC). A continuous-time Markov chain is a term for a continuous-time process (CTMC). It bears Andrey’s name, a Russian mathematician, Markov(Wikipedia).
In this case, Midi data should be given into the analyzer by reading a midi file and providing its pitch input. Based on the current state and a set of probabilities, Markov Chains determine the following state. If this were mapped to pitch, selecting our next note would include taking into account both our present note as well as a list of potential notes and their probability.
Markov Chains choose the next state based on the current state and a set of probabilities. As an example, here are the notes of ‘Happy Birthday’:
- C4 C4 D4 C4 F4 E4
- C4 C4 D4 C4 G4 F4
- C4 C4 C5 A4 F4 E4 D4
- Bb4 Bb4 A4 F4 G4 F4
The next note in a First Order Markov Chain is determined by the current note and a set of probabilities. We can learn about the likelihood of one note following another by analyzing Happy Birthday. This table’s first column displays all of the notes in the song, followed by a list of numbers representing all of the notes that followed that pitch.
- C4, C4 D4 F4 C4 D4 G4 C4 C5;
- D4, C4 C4 Bb4;
- E4, C4 D4;
- F4, E4 C4 E4 G4;
- G4, F4 F4;
- A4, F4 F4;
- Bb4, Bb4 A4;
- C5, A4;
As a result, C5 was only followed by A4. Probabilities between 0 and 1 can be measured. The likelihood of A4 being followed by C5 is one, as is the probability of A4 being followed by F4. Typically, this is represented by a table displaying the following probabilities:

This table is known as a transition matrix, a state transition matrix (STM), or a transition table.
Once we have this information, we can develop fresh material based on these probabilities. The STM can be generated by manually or by analyzing existing music or data. For example, you could load up all of Mozart’s works and construct algorithmic compositions using the same set of note probabilities.
In this post, we’ll look at how to use PureData to automatically analyze a MIDI file and build a first order STM, which we’ll then use to construct some simple algorithmic music compositions. We’ll only use pitch in this example, but you can easily extend it to include rhythm, dynamics, or other musical components.
Bulding Markov Chain Analysis core
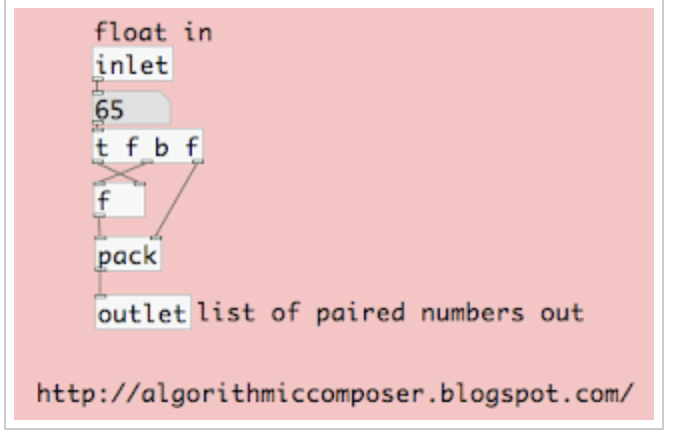
Our new matrix is saved in a data object known as a coll. When you refer to a coll with the same name (in this case, pitchMatrix), it retrieves the same data.

Inside pd pair
Pitch generator
Now we can generate pitches based on transition values. Beginning with a single note from our input melody, we use the length object to determine the length of the list of possible future notes. This is used as input to the random object, which selects a number at random and then selects one of the following notes from our own pitchMatrix object. In our STM MIDI, for example, if note 60 is followed by 64 62 64 65, there is. There is a 5% probability of picking 64 and a.25 chance of picking 62 or 65.