Cellular Automata - Implementation in Pure Data
“If you couldn’t predict what it did, then probably that’s because it was capable of doing anything.”
– John Conway on his 2-D grid Cellular Automaton called “The Game of Life”

Years ago I stumbled upon an idea in mathematics which caught my attention: Cellular Automata - simple, easy to understand systems which are observed to produce complex behavior. I researched on it, had some fun with its gamy applications on the web but soon put it in the category ‘filed for memory’. The day came, and while I was programming my synthesizer for the course in Pure Data, I remembered. Could this be applied in PD? At the end of this blog you can see my Pure data patch in action. But wait, what are Cellular Automata (CA)?
Cellular Automata Explained
Stanisław Ulam and John Von Neumann conceived the idea. In an effort to formulate a theoretical model to describe self-replicating robots(!!!), von Neumann looked for a concept that would work. The model wasn’t complete until his colleague Ulam suggested using a cell-based approach - Cellular Automata were born. I’ll go over the fundamentals with you in the following.
Consider the idea of a theoretical robot that is a collection of cells on an n-dimensional grid. Each cell can be in a finite number of states and has a specific number of neighbours. The state of a cell is determined by the state of its neighbours. If we apply discrete-time steps (like generations) each cell state will change in relation to its neighbour states.
Let’s try to imagine the simplest form of a Cellular Automaton.
A one-dimensional grid with cells
a cell can either be dead (1) or alive (0)
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
each cell’s state depends on its two neighboring cells

Let’s summarize: a CA in its simplest form is a one-dimensional grid of cells that evolves over time. Each cell has a state, 0 or 1, dead or alive, and a neighborhood consisting of two other cells. Stephen Wolfram initially described this most simplest of CA’s in his gigantic groundbreaking book ‘A New Kind of Science’ ,which you can access online for free if you dare.
But, depending on the neighbour cells, how do we decide a cell’s state? If we look closely, we see that three cells represent a 3-digit number in binary, so 2³ = 8 possible combinations.

Now, we need to define a ruleset to determine the middle cell’s state for the next generation. We use each combination from above once and determine an 8-bit number.

Turns out there are 256 combinations - 2⁸ – and Stephen Wolfram systematized them by their corresponding binary number.

If we now add time to the equation and iterate over the grid and change each cell’s state with a new generation we get this. The starting condition is a single cell with a 1 - a seed.

We could also add a new row for each new generation and we get the following for rule 90.

The grid evolves a pattern over time! It is an example of a set of simple rules that can produce complex behavior and I think the idea is beautiful.

Conway’s game of life

I want to introduce an implementation – certainly the most famous one- of the idea on a 2 -dimensional grid – the Game of Life (listen to John Conway’s retrospective on his creation.) It is fun watching it evolve over time, and most importantly, it is Turing complete which allows it to do this. With a balanced but simple set of rules it is capable of universal computation!
The following table shows Stephen Wolfram’s behaviour classification for the elementary rule sets according to their outcome over time. The same classification can be applied to 2-D Cellular Automata.
| Class1 : Stable | Class 2: Repetitive or Stable | Class 3: Random | Class 4: Complex | |
|---|---|---|---|---|
| 1 D | Rule 222  |
Rule 90  |
Rule 30  |
Rule 110  |
| 2 D | Aircraft Carrier  |
Gosper Glidergun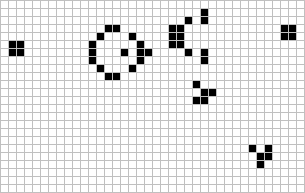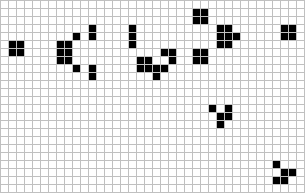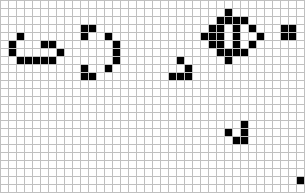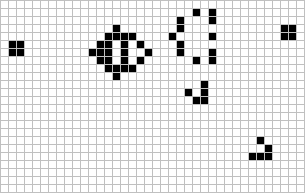 |
Switch Engine (initial state) |
The concept of Cellular Automata has extensive usecases, for example in pattern recognition, theoretical modelling, encoding (Rule 30 as a pseudorandom number generator) or – Music.
Cellular Automata represent a type of computational thinking I can really relate to. My Pure Data patch is a prototype for a final module I like to use for composition. It can only produce rule 90 at the moment, which is a Class 2 CA so it’s repetitive, and consists of 16 cells, but I aim at making it generic depending on input and give it more cells. Anyway, the current state is great for defining rhythmic patterns or melody lines without having too much randomness in there. And it blinks quite nice. Give it a listen down below.
CA module and parts of other patches play together. Check my github for the file.
