Ambisonics: Under the Hood
Introduction
Ambisonics is a spatial audio format that enables a quick and easy creation of a 3D audio mix. We created a video tutorial to show you how to create an Ambisonics mix using Reaper and the IEM plugin suite, which you can watch below.
This blog post goes into a little more detail in how exactly Ambisonics works and why Ambisonics is speaker independent, for those interested in what is going on ‘under the hood’.
The Channel Based Approach
When traditionally mixing, we assign track information to a channel of audio, and each channel is reproduced over a speaker. This approach is carried over for traditional surround formats. So in a 7.1 setup, for example, we mix using eight channels, assigning our different channels to each track to create the spatialisation effect that we desire, and then sending each track to an individual loudspeaker. This is called a channel based approach. However, this can lead to problems when we don’t have 8 loudspeakers to playback our mix. What do we do with the extra channels if we have fewer speakers? And what if they’re in a different configuration to the setup on which the mix was created? Ambisonics offers a solution, in that the mix is speaker independent. This means that your mix can be played back over whatever loudspeaker configuration you have available. Let’s examine how this is possible!
The Ambisonics Approach
In contrast to a channel based approach, in Ambisonics we don’t mix by assigning a track to a channel, but rather we mix by placing a sound source on the surface of a spherical soundfield. We then encode this soundfield into a format called b-format where each channel carries the information of a spherical harmonic of the soundfield. These can be used to reconstruct the soundfield onto our loudspeaker array through the use of a decoder. A useful way of thinking about this is that when mixing, we’re creating a virtual soundfield, and through the use of the encoder we are ‘recording’ portions of this soundfield that we then reproduce for playback when decoding. Let’s look at an example of this.
Recording the Soundfield
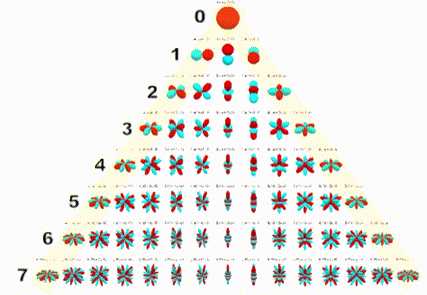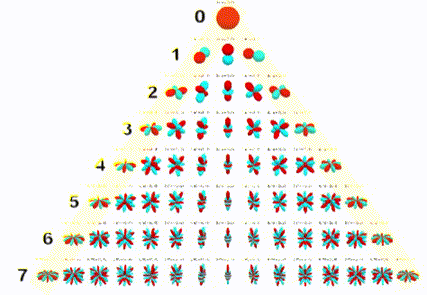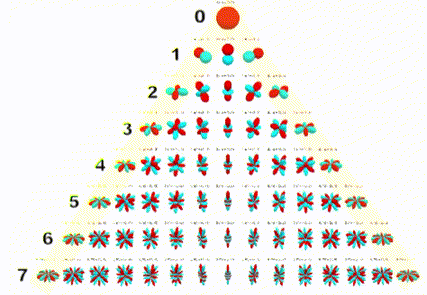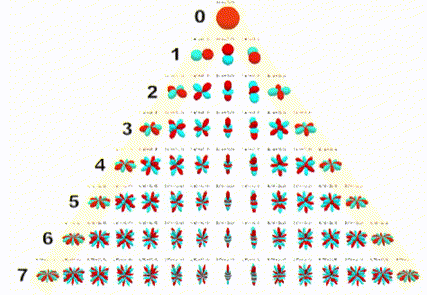
In the visual below, we can see the spherical harmonics up to the seventh order.
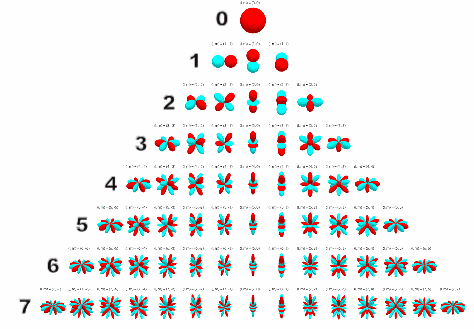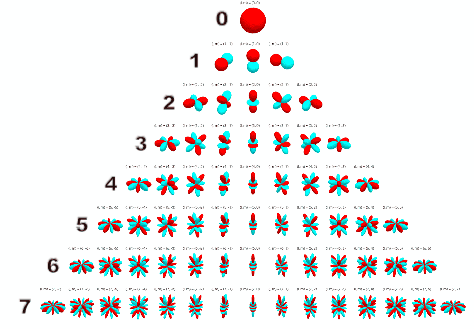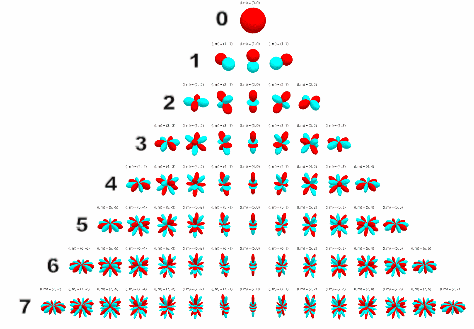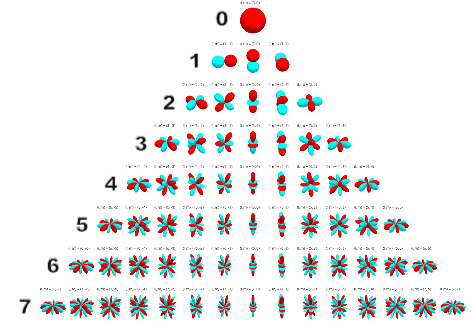
If you’ve had experience with microphones, the zeroeth and first order spherical harmonics should look familiar, resembling an omnidirectional and figure-of-eight polar pattern respectively.
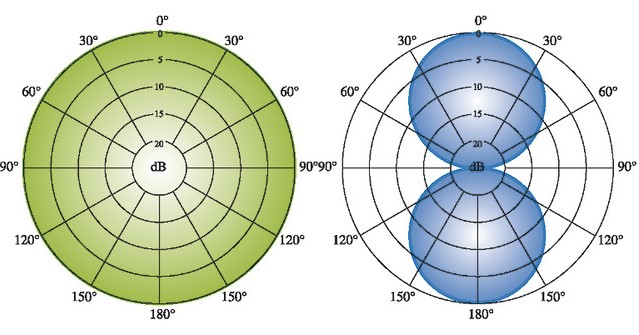
And this is correct! If we placed an omnidirectional microphone and three figure-of-eight microphones (each pointing along a different Cartesian axis) at the same point, we would record the spherical harmonics of the soundfield up to the first order, and could then decode this as Ambisonics! So if we encode our soundfield to preserve the first four spherical harmonics, we are in effect ‘recording’ our virtual soundfield using the microphone setup described above. As the order of the spherical harmonics increases, these ‘polar patterns’ become more complex, but can still fundamentally be thought of as the portion of our soundfield that we are ‘recording’.
Intuitively, the more spherical harmonics we have, the more accurately we can reproduce our soundfield, thereby increasing the ease of sound source localisation and the size of the ‘sweet spot’. When choosing the order of Ambisonics, we are actually deciding the number of spherical harmonics that we are ‘recording’. So if we choose to encode in first order Ambisonics, we are ‘recording’ the first four spherical harmonics, in third order the first 16, and so on. As we need a channel for each harmonic, we can find the number of channels we need for an order by using the following formula:
So to encode seventh order Ambisonics, we would require
channels.
Soundfields in 2D
If we only want to reproduce a 2D soundfield, the number of required channels is dramatically reduced. We don’t need to ‘record’ any of the vertical information, and so only need to encode the spherical harmonics which include horizontal information. If we take a seventh order encoding as an example, we would only need the harmonics highlighted below.
We can find the number of channels we need for a 2D encoding using the following formula:
So for a seventh order encoding, we need
channels.
However, remember that even in 2D, for first order, you still need a minimum of four channels.
Summing Up
- When we mix for Ambisonics, we place objects in a virtual spherical soundfield.
- We then decide which spherical harmonics of the soundfield we wish to preserve by encoding the soundfield into b-format at a desired Ambisonics order. We can think of this as ‘recording’ portions of the soundfield with microphones that have polar patterns corresponding to the harmonic.
- As each harmonic requires a channel for encoding, we can use the formulas above to find how many channels we require for the order that we have chosen.
- When we decode the b-format, we are choosing which harmonics to reproduce. We can decode at a lower order (and therefore for fewer speakers) than we encoded in because the information of the lower order harmonics is still contained in the b-format signal.
Sources and Further Reading
Arteaga, D. (2015). Introduction to Ambisonics.
Zotter, F., & Frank, M. (2019). ‘XY, MS, and First-Order Ambisonics’. Ambisonics: A Practical 3D Audio Theory for Recording, Studio Production, Sound Reinforcement, and Virtual Reality, pp. 1–22. Springer International Publishing: Cham. DOI: 10.1007/978-3-030-17207-7_1
Image Sources
https://upload.wikimedia.org/wikipedia/commons/7/74/Real_Spherical_Harmonics_Figure_Table_Complex_Radial_Magnitude.gif
https://dt7v1i9vyp3mf.cloudfront.net/styles/news_large/s3/imagelibrary/Q/QA_4-0811-qSuciyY05bdnpJjU8IQDmj8ZBfB.PaBl.jpg
Video Tutorial Media Sources
Audio
Angels in Amplifiers - I’m Alright; From https://www.cambridge-mt.com/ms/mtk/
Images
https://notam.no/wp-content/uploads/2019/10/siriusoriginal-studio3Web.jpg
https://notam.no/wp-content/uploads/2016/09/SiriusstWeb.jpg
https://blog.bestbuy.ca/wp-content/uploads/2016/07/44354i9E45BD1951EE047B.jpg
https://dxarts.washington.edu/sites/dxarts/files/styles/large_full_width/public/images/dxarts_media_lab1_sm.jpg?itok=UlD5573s
https://upload.wikimedia.org/wikipedia/en/f/f6/AmbisonicLogo.svg
https://www.researchgate.net/publication/341128068/figure/fig1/AS:887453950939143@1588596918992/Ambisonics-spherical-harmonics-for-orders-up-to-three-FOA-includes-the-top-two-lines-of.png
https://ocl-steinberg-live.steinberg.net/_storage/asset/60417/storage/JPG_large_2000px/60417-large.jpg
https://i.imgur.com/Ts2fWMx.png
https://i.ytimg.com/vi/l0sxyrAuB0k/maxresdefault.jpg
