Scale over Chord using ANN

Introduction

The aim of this research is to propose a way of determining the usable scale(s) in any jazz harmonic context, according to what scale choice a particular great soloist would have made. It is to be proven that some chord components may favor a certain scale choice over another.

Most of the music theory relies on Mark Levine’s jazz theorizing (Levine 1995), but only the heptatonic scale is considered. The simplified model used here consists of categorising chords and scales into six types. A different algorithm should be trained for each type and each missing degree, but the 6th of dominant chords (mixolydian and mixolydian b13) will be used as a proof of concept here.

Database

The Weimar Jazz Database (Pfleiderer 2017) contains manual transcriptions of 456 famous jazz monophonic solos. One of them, Benny Goodman’s improvisation on Handful of Keys, is shown in fig. 1 as a PDF score.

Fig. 1: Handful of Keys as a score

In the database, chords are represented as strings, and notes as MIDI pitches. Notes that are missing harmonic context (notated N.C.) are simply discarded. Fig. 2 reveals what exact data is being retrieved from Handful of Keys (song no 15 in the WJazzD).

Fig. 2: Handful of Keys as a data set

Implementation

A regression algorithm is used here, where the target is a float between 0 (minor) and 1 (major) representing the 6th’s major alteration’s probability on a dominant chord.

Libraries

To do the music theory analysis (parse chords, compare notes, construct scales, …), a custom library has been implemented.

To retrieve the data from the WJazzD database, sqlite3 is used.

Target Definition

The target float in this implementation represents the probability between two cases, major and minor alteration of the 6th (of dominant chords). As the same harmonic contexts (features) can lead to different outputs, data with similar features are used to calculate a proportion for each output.

Feature Extraction

The features represent the harmonic contexts of any chord. Many notations and neighbour sizes have been tested, but the one that gave the best results uses pitch classes (Rahn 1980):

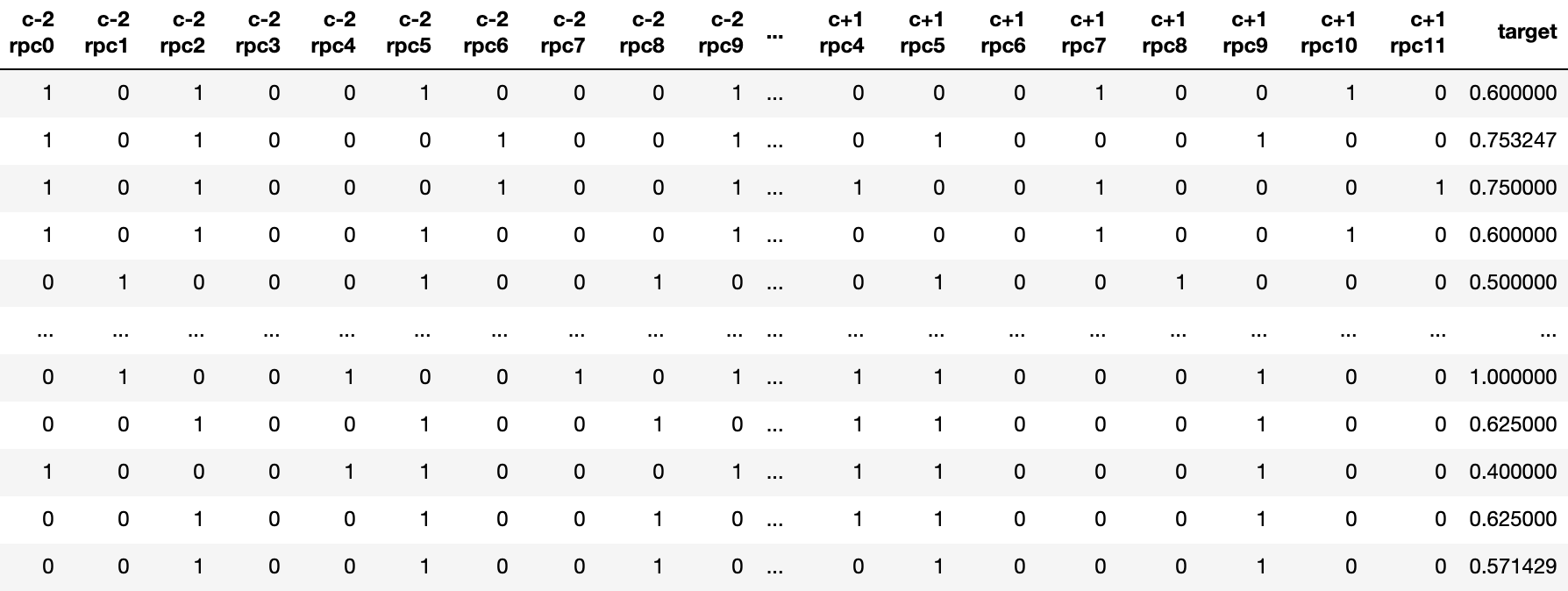
For any central chord numbered c in the progression, the harmonic context is defined as the relative pitch classes of the chord notes composing the chords numbered c-2, c-1 and c+1 (2 chords before, 1 chord after).

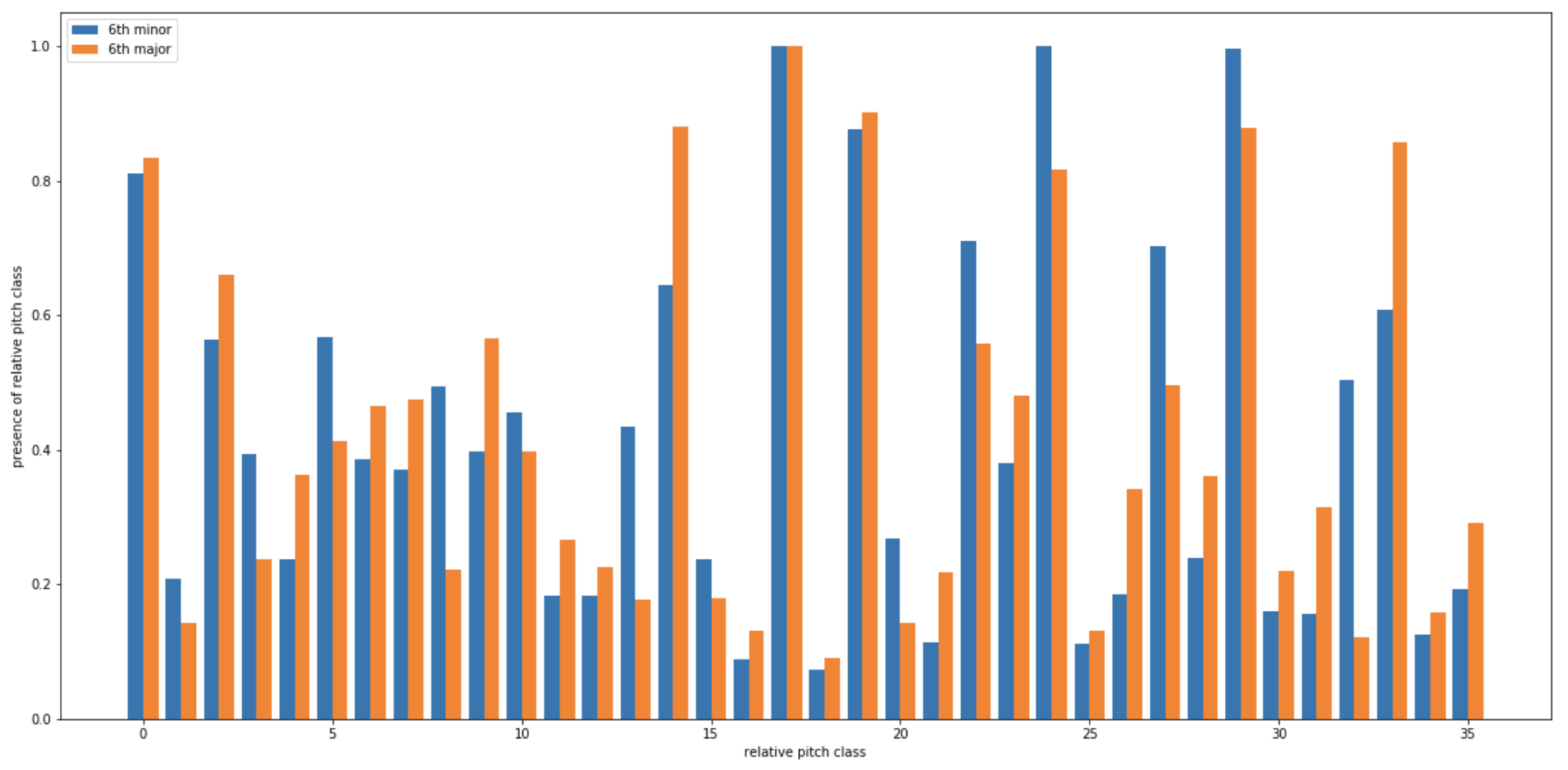
The relative pitch classes (rpc) are defined as the difference (%12) between the chord notes’ pitch classes and the pitch class of the current chord’s fundamental. Fig. 3 shows a sample of features associated to a target. Fig. 4 aims to represent the data set by showing the slight differences between major and minor 6th cases in the WJazzD.

Fig. 3: Features and target
Fig. 4: Proportion of each rpc for each neighbouring chord, classed by most probable alteration

Algorithm

An artificial neural network is used to train the data with, as it seems to be a scalable solution, in case this project goes any further. The underlying task of the model is to define which neighbouring relative pitch classes tend to imply a major or minor 6th alteration, particularly which are the defining relative pitch classes. The assumption was that some notes present in the neighbouring notes would influence the scale selection, and it seems to be the case as the algorithm gives coherent results.

Evaluation

At first the testing gave r2 scores around 0.5, which is not too bad for a start. Neural networks were given a size of 2 layers containing between 4 and 16 neurones. Doing repeated k-Fold and grid search quickly revealed that parameters tweaking could enhance the results quite significantly. Splitting the data in 0.8 for training and 0.2 for testing, using an activation parameter ‘tanh’ and hidden layer sizes of [300, 300, 300, 300, 300, 300, 300], the testing gives a r2 score of around 0.65, which can be considered a significant increase. The variance is quite low, the training always gives r2 scores between 0.62 and 0.67.

The system is of course enhanceable, but the result seems to indicate that there is indeed a correlation between the harmonic context and the alterations of the heptatonic missing degrees.

Reflection

One of the main benefits of the research is its application to the existing AutoScale improvisation system (Jaccard 2020). Indeed, this software aims to predict and propose scales on any chord progression, which could now be done using machine learning trained on any great jazz artist.

If the project goes any further, models have to be trained separately to determine alterations of any degrees of any chord type (not just dominants’ sixths). Furthermore, the particular jazz artist could be considered as a new feature, and the scale proposition algorithm could be inspired by any improviser the user wants to imitate, or learn from.

Conclusion

This project has been a great pedagogic opportunity, as I learned so many basic aspects of machine learning and more specifically data retrieval and feature extraction. I really want to carry on in this direction, and use this first step as a start in my master thesis. I in fact consider creating a bigger database derived from audio recording, containing both chord and scale progressions. In such a process, the WJazzD could be considered as a testing data set.

References

  • Rahn, J 1980, Basic Atonal Theory, Longman, New York.
  • Levine, M 1995, The jazz theory book, O’Reilly Media, Inc., Surrey.
  • Pfleiderer, M 2017, Inside the Jazzomat - New Perspectives for Jazz Research, Schott Campus, Mainz.
  • Jaccard, T 2020, AutoScale: Automatic and Dynamic Scale Selection for Live Jazz Improvisation, NIME.